Assignment III: MPI Programming

For each exercise:

• Compile a short report according to instructions, and answer questions that are marked Question(s).
• Submit your code to a GitHub repo (write the link in the report).
• Presentation booking will open around the deadline of the assignment. More info here.
• All the code used in this assignment can be found here: https://github.com/KTH-HPC/DD2356/tree/master/Assignment-III Links to an external site.
• The assignments must be done using Beskow. Make sure to compile and run programs on Beskow correctly to pass the assignment. Read Compiling and Running a Job on Beskow very carefully.
• The Beskow allocation (core hours and priority) is shared between all the students in the class. Be considerate and only allocate when you need to run jobs on the compute nodes. Do not, for example, open many terminals and salloc them all for your own convenience while leaving them idle. When finished using an interactive allocation (with salloc), remember to exit to return the nodes.

---

Exercise 1 - MPI Hello World

Here we’re going to implement our first MPI program. The goal is to get familiar with the MPI environment.

Expected knowledge includes a basic understanding of the MPI environment, how to compile an MPI program, how to set the number of MPI processes, and retrieve the rank of the process and number of MPI processes at runtime.

Instructions. Write a C code to make each MPI process print "Hello World from rank X from n processes!", with X = rank of the MPI process and n = total number of processes. Learn how to launch an MPI code on Beskow.

Your code using 4 MPI processes should behave similarly to:

Write a hello world code in C with the following output:

Hello World from rank 3 from 4 processes!
Hello World from rank 0 from 4 processes!
Hello World from rank 2 from 4 processes!
Hello World from rank 1 from 4 processes!

Questions

1. Write the code in C.
2. How do you compile it, which compiler and flags have you used if any?
3. How do you run the MPI code on Beskow?
4. How do you change the number of MPI processes? 
5. Which functions do you use for retrieving the rank of an MPI process and the total number of processes?
6. What are the names of the most used MPI implementations?

---

Exercise 2 - 1D Domain Decomposition with Blocking Communication

Expected knowledge includes a basic understanding of MPI point-to-point communication.

One of the most common techniques in parallel computing is called domain decomposition. When we solve partial differential equations (think about the Poisson equation or the wave equation), using finite difference or finite element techniques, we introduce a computational grid in the domain: at each point of the grid, the values of our variables are defined. For instance, we have a one-dimensional computational grid that consists of nine cells and three MPI processes, we can divide the grid into three smaller grids (called domains) and assign them to each process. The first MPI process (rank 0) will have the variables associated with the first three cells 1-3, the second MPI process (rank 1) will store the variables for cells 4-6, and the third MPI process (rank 2) will store the variables for cells 7-9. Note the values are defined on the nodes (vertical bars in the plot below) are the same values, albeit on different domains.

One problem we might have is that one MPI process requires the values available on the adjacent processes. For instance, we want to calculate a numerical derivative on a point at the edge of the domain, we will need to know the value defined on the adjacent domains. To address this problem, at the edges of the domains two additional nodes are added. The additional cell and nodes are called ghost (or halo) cells. These ghost cells will host the values defined on the adjacent cells and are required for the calculation. A diagram of how the domain decomposition work is shown below.

   

In the domain decomposition, before performing the computation, we communicate with MPI and fill the ghost cell values. For instance, communication can be divided into two stages: in the first stage, each process communicates the values for the ghost cells on the right of the domain to the MPI processes having the domain on the right;  in the second stage, each process communicates the values for the ghost cells on the left of the domain to the MPI processes having the domain on the left.

The goal of this exercise is to implement the communication for the 1D domain decomposition using MPI blocking point-to-point communication. In particular, we are going to calculate the first-order derivative of the function sin(x) on a domain spanning from 0 to L. Each MPI process will calculate the derivative using the central finite difference technique. However, before the calculation, we need to implement the MPI communication for storing the correct values on the ghost cells.

To implement the 1D domain decomposition, you can start from the code domainDecom1D.c Download domainDecom1D.c

  

Questions. Here the steps you need to follow for the exercise submission:

1. Implement the communication for the 1D domain decomposition using MPI blocking point-to-point communication. Assume periodic boundary conditions, e.g. the first and last process will communicate.
2. Test the results by checking the correct values are on the ghost cells and the derivative of sin(x) on the edges of the domain is correct (the derivative of sin(x) is cos(x)). Show how you implement this checking. (We will ask to demonstrate during the lab presentation.)
3. Why MPI_Send and MPI_Recv are called "blocking "communication?

---

Exercise 3 - Measure Network Bandwidth and Latency on Beskow with Ping-Pong

Expected knowledge is concepts of bandwidth and latency and performance model for parallel communication.

The ping-pong is a benchmark code to measure the bandwidth and latency of a supercomputer. In this benchmark, two MPI processes use MPI_Send  and MPI_Recv  to continually bounce messages off of each other until a final limit.

The ping-pong benchmark provides as output the average time for the ping-pong for different message sizes.

If we plot the results of the ping-pong with size on the axis and ping-pong time on the y-axis, we will roughly obtain points distributed along a line. If we do a linear best fit of the obtained points, we will get the intercept and the slope of the line. The inverse of the line slope is the bandwidth while the intercept is the latency of the system.

We will use the following code Download code

to measure the ping-pong time for different message sizes.

Instructions.  For completing this exercise, make sure to check Lecture: Performance Modeling & Ping-Pong.

Run the ping-pong code and calculate the bandwidth and latency for:

1. intra-node communication (2 processes on the same node)
2. inter-node communication (2 processes on different nodes)

Questions. Here the steps you need to follow for the exercise submission:

1. Run the ping-pong benchmark for 1) and 2). After that, plot the ping-pong time in function of the message size in 1) and 2). 
2. Using best fit (using Matlab, Python, or similar), calculate the bandwidth and latency for 1) and 2).
   • Hint: if you obtain a negative number for latency, you can omit the ping-pong times for small message sizes. In fact, the measurements for small messages are quite noisy.
   • Important note: If you still obtain a negative latency, use 1.6 microseconds (1.6E-6s) for internode communication and 0.7 microseconds for intra-node communication when developing a performance model for the network communication. These are values that we have measured on Beskow in previous tests. 
3. Modify the ping-pong to test use MPI one-sided communication instead of point-to-point communication. You can follow the direction at https://cvw.cac.cornell.edu/mpionesided/pingpong Links to an external site.
4. What is the difference between one-sided communication and point-to-point (two-sided) communication?
5. Calculate the latency and bandwidth using the one-sided ping-pong test. Compare and discuss the difference of performance between MPI one-sided and point-to-point communication.
6. Read Modeling MPI Communication Performance on SMP Nodes: Is it Time to Retire the Ping Pong Test paper and answer the following questions:
   1. Why the postal model is not the best performance model for communication?
   2. Which proposed performance model is proposed?

---

Exercise 4 - Calculate PI with MPI

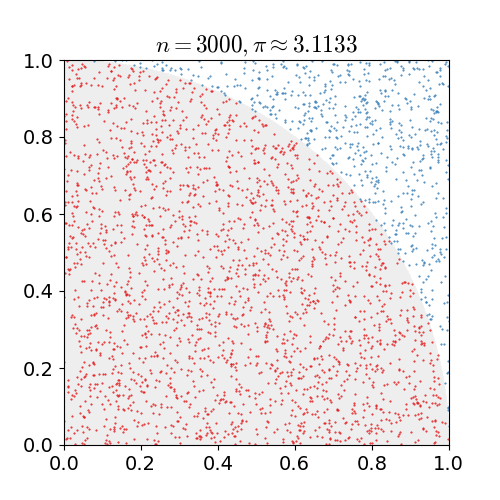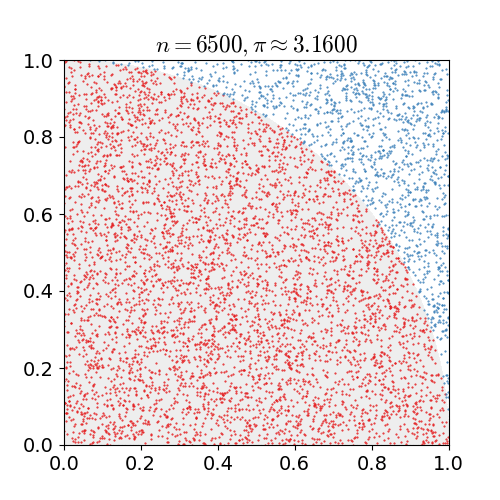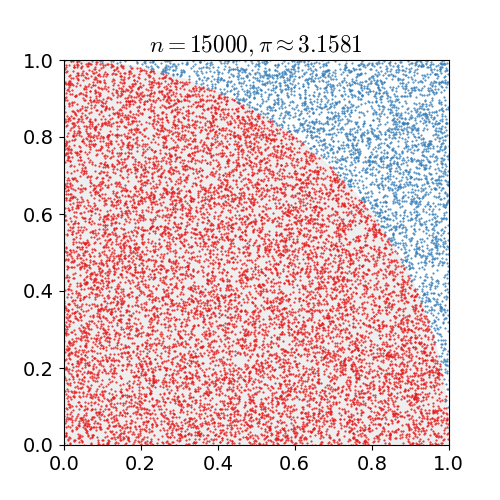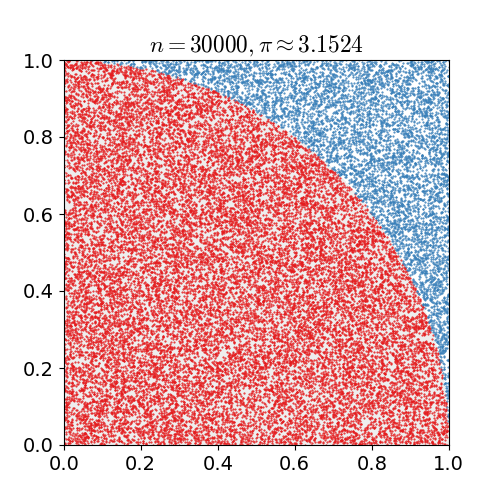
In this exercise, we are going to parallelize the calculation of Pi following a Monte Carlo method and using different communication functions and measure their performance.

Expected knowledge is MPI blocking and non-blocking communication, collective operations, and one-sided communication.

Instructions. Write different versions of MPI codes to calculate pi. The technique we are implementing relies on random sampling to obtain numerical results.  The basic MC algorithm is based on the following steps:

1. Draw a unit square
2. Draw a unit circle inside the unit square
3. Throw a coin in the unit square
4. Count the rate of success where the coin ends up in the unit circle: P(coin in the circle)

• • P(coin in the circle) = area of the circle/area of the square = $\frac{\pi r^2}{(2r)^2}=\frac{\pi r^2}{4 r^2}=\frac{\pi}{4}$
    • --> π = 4 P(coin in the circle)

The serial code (courtesy of ORNL) we are going to parallelize is provided here Download here

.

4.1  MPI Blocking Communication & Linear Reduction Algorithm

In our parallel implementation, we split the number of iterations of the main loop into all the processes (i.e., "NUM_ITER / num_ranks"). Each process will calculate an intermediate count, which is going to be used afterward to calculate the final value of Pi.

To calculate pi, you need to send all the intermediate counts of each process to rank 0. This communication algorithm for reduction operation is called linear as the communication costs scale as the number of processes.

An example of linear reduction with 8 processing is the following:

Rank 0 is going to receive the intermediate count calculated by each process and accumulate them to its own count value. Finally, after rank 0 has received and accumulated all the intermediate counts, it will calculate Pi and show the result, as in the original code.

Implement this code using blocking communication and test its performance.

Hint 1. Change the main loop to include the number of iterations per process, and not NUM_ITER (which is the total number of iterations).

Hint 2. Do not forget to multiply the seed of srand() with the rank of each process (e.g., “rank * SEED”) to ensure the RNGs of processes generate different random numbers.

Questions. Here the steps you need to follow for the exercise submission:

1. Implement the code using a linear algorithm with MPI Send/MPI_Recv
2. Measure the performance of the code (execution time) for 8, 16, 32, 64, 128, (possibly 256) MPI processes and plot it. How the execution time scale with the number of processes? What is the MPI function for timing?
3. Develop a performance model for the execution time of the application (or of the communication model only) using the postal communication model for the network performance. Use the values of bandwidth and latency you found in exercise 2. Compare the results from the measurements with the performance model results.

4.2 MPI Blocking Communication & Binary Tree Reduction Communication Algorithm

Implement the binary tree communication algorithm for performing the reduction on rank 0 using blocking communication, e.g. MPI_Send / MPI_Recv.

The communication pattern for a reduction with a binary tree with 8 processes is the following:

In our implementation, we can assume that we use a power of 2 number of processes.

Questions. Here the steps you need to follow for the exercise submission:

1. Implement the code using a binary tree algorithm with MPI Send/Recv
2. Measure the performance of the code (execution time) for 8, 16, 32, 64, 128, (possibly 256) MPI processes and plot it
3. Develop a performance model for the execution time of the application (or of the communication model only) using the postal communication model for the network performance. Use the values of bandwidth and latency you found in exercise 2. Compare the results from the measurements with the performance model results.
4. How does the performance of binary tree reduction compare to the performance of linear reduction?
5. Increasing the number of processes - let's say 10,000 processes - which approach (linear/tree) is going to perform better? Why? Think about the communication performance model.

4.3  MPI Non-Blocking Communication & Linear Reduction  Algorithm

Use non-blocking communication for the linear reduction operation (4.1).

Hint: Use a non-blocking MPI_Irecv(). The basic idea is that rank 0 is going to issue all the receive operations and then wait for them to finish. You can either use MPI_Wait() individually to wait for each request to finish or MPI_Waitall(). Regardless of your decision, keep in mind that we want you to perform the receive operations in parallel. Thus, do not call MPI_Irecv() and immediately MPI_Wait()! In addition, we recommend you allocate an array of MPI_Request and also an array of counts (i.e., one for each receive needed).

Questions. Here the steps you need to follow for the exercise submission:

1. Implement the code using non-blocking communication.
2. Measure the performance of the code (execution time) for 8, 16, 32, 64, 128 (and possibly 256 ) MPI processes and plot it
3. What are the MPI functions for non-blocking communication? What does the "I" in front of the function name stand for in non-blocking communication?
4. How the performance of non-blocking communication compares to the performance of blocking communication. e.g. performance results in 4.1?

4.4 MPI Collective: MPI_Reduce

Use the collective MPI_Reduce operation.

Hint 1: Remember that the goal of MPI_Reduce is to perform a collective computation. Use the MPI_SUM operator to aggregate all the intermediate count values into rank 0, But, watch out: rank 0 has to provide its own count as well, alongside the one from the other processes.

Hint 2: The send buffer of MPI_Reduce must not match the receive buffer. In other words, use a different variable on rank 0 to store the result

Questions. Here the steps you need to follow for the exercise submission:

1. Implement the code using MPI_Reduce
2. Measure the performance of the code (execution time) for 8, 16, 32, 64, 128 (and possibly 256) MPI processes and plot it.

---

Exercise 5 - iPIC3D Performance Monitoring with MAP

In this exercise, we are going to monitor the performance of a scientific application using MPI by using a tool, called Allinea (now ARM) MAP. MAP is an application profiler by Arm (formerly by Allinea Software). The profiler is able to profiler the performance of C, C++, Fortran, and Python software. It offers many profiling capabilities such as MPI profiling and OpenMP profiling on large-scale systems. The use of the profiler requires a license but it is already installed on many large systems such as Beskow. After our application returns, a file with .map extension will be generated. We can transfer this file to your remote client for visualization and analysis. For the installation of the viewer on your laptop and workstation and different breakdown views, please consult Tutorial: Profiling of MPI Applications.

For this exercise, we are going to run an MPI application, generate the traces with the profiling information, and visualize them. The scientific application we are going to monitor is iPIC3D, a Particle-in-Cell code for space plasma simulations. The first step of this exercise is to download and build on Beskow the iPIC3D code. You can download the source code and instructions to build it at https://github.com/KTH-HPC/iPIC3D Links to an external site..

Once you have built successfully iPIC3D, you can run it on Beskow using 8 MPI processes and the input file testGEM3Dsmall.inp. The code will run for 51 cycles.

We will use the Intel environment. Do exactly the following to compile the code (but if you face segfault issue when running the code, ignore the loading of cray-hdf5 module):

$ module swap PrgEnv-cray PrgEnv-intel
$ module load cray-hdf5
$ module load allinea-forge/20.0.3
$ git clone https://github.com/KTH-HPC/iPIC3D.git
$ cd iPIC3D
$ mkdir build && cd build
$ CC=cc CXX=CC cmake -DCMAKE_EXE_LINKER_FLAGS_INIT="-lmap-sampler" ..
$ make

To generate the traces with MAP, we will run the program as usual, but prepend the map --profile before srun.

$ mkdir data
$ salloc -A edu21.dd2356 -t 00:05:00 -N 1 -C Haswell
salloc: Granted job allocation
$ map --profile srun -n 8 ./iPIC3D ../inputfiles/testGEM3Dsmall.inp
Arm Forge 20.0.3 - Arm MAP
....
MAP analysing program...
MAP gathering samples...
MAP generated iPIC3D_8p_1n_2021-04-27_10-41.map


*** SIMULATION ENDED SUCESSFULLY ***
 Simulation Time: 2.35613 sec (0.000654481 hours)
***

The map dump will be in the same directory. Transfer it to your local workstation to visualize with the viewer.

Questions. Here the steps you need to follow for the exercise submission:

1. By running MAP with iPIC3D, generate the .map traces. Move the .map file to your laptop or workstation and visualize it using the MAP viewer. Take a screenshot of the visualization of the MAP results and add it to the report.
2. What are the iPIC3D functions that take most of the time? Check the MAP breakdown of different activities
3. What is the recorded bandwidth of MPI Sent and Received?

---

Bonus Exercise - Distributed Matrix Multiply with the Fox Algorithm

One of the most important kernels in HPC is matrix-matrix multiplication. In one of the first module lectures  (Lecture: Matrix-Matrix Multiply), we investigated the matrix-matrix multiplication with a serial code and looked at the nature of the kernel (computation vs memory operation) and possible optimizations.

The goal of this project is to develop, analyze the performance, and optimize a distributed-memory version of double-precision matrix-matrix multiply using MPI. In particular, we are going to implement an algorithm introduced by Goeffrey Fox in a seminal paper:

• Fox, G.C., Otto, S.W. and Hey, A.J., 1987. Matrix algorithms on a hypercube I: Matrix multiplication. Parallel computing, 4(1), pp.17-31.

Before starting the project, make sure to read this paper, freely available here:

B1. The Fox Algorithm

• Matrix algorithms on a hypercube I: Matrix multiplication
  • G.C Fox and S.W Otto and A.J.G Hey p. 17 - 31. 1987
  • Optimized for systems with a mesh topology
• Tile-based distributed matrix multiplication
  • Divide matrix using grid decomposition
  • Each process holds a tile of matrix A and B where $C=AB$ 
• Use exact same matrix multiplication algorithm for each tile
  • Performs matrix multiplication on tiles 
  • Accumulate the result in the C tile

The steps of Fox's algorithm are the following:

1. Broadcast the diagonal tile of A in a horizontal direction.
2. Multiply the copied A tile into the B tile currently residing in each processor.
3.  'Roll' the B tiles vertically: Send current tile B to the process holding the tile “above” current tile + Receive new tile B from the process holding the tile “below” current
4. Do a horizontal broadcast of the 'diagonal + 1' tiles of A.
5. Multiply the copied A tiles into the currently residing B tiles.

Continue this pattern until B has 'rolled' completely around the machine (this would require sqrt(n_tiles) iterations)

B1.3 Problem Decomposition (step 1)

Perform domain decomposition of the matrices to tiles according to the number of the processors used.

B1.4 The Whole Matrix-Matrix Multiply

B1.5 First Iteration: Broadcast main diagonal - matmul - send B tile to process "above" and receive from "below"

After the matmul, each tile is sent to the above process and receive from the bottom process. Think of it as rotating vertically.

B1.6 Second Iteration: Broadcast +1 diagonal - matmul - send B tile to process "above" and receive from "below"

After the matmul, each tile is sent to the above process and receive from the bottom process.

B1.7 Third Iteration:  Broadcast +2 diagonal - matmul - send B tile to process "above" and receive from "below"

B2.  Implementation 

In the implementation, you can assume that:

• Matrices are square
• Tile size depends on the number of processes
• The number of processes must be a square

B2.1 Implementation Possibility: Broadcast of tile to the same row

There are different ways to implement a broadcast to processes on the same row. One possibility is to implement a linear broadcast with MPI send/recv. A Cartesian virtual topology might help in calculating the coordinate of the processes in the grid.

A more elegant solution would be to use MPI broadcast to a subset of the processes (same row processes). To create a sub-communicator with:

• Cartesian communicator; OR
• MPI Communicator split

Useful MPI functions are:

• MPI_Bcast()
• MPI_Cart_create()
• MPI_Cart_sub()
• MPI_Cart_shift()
• MPI_Comm_split()

B2.2 Implementation Possibility: "Roll" of B tiles

Compute rank of process “above” with

• • • Simple modulo operation; OR
    • Create column communicator from Cartesian communicator and shift

Possibly, useful MPI functions are:

• MPI_Bcast()
• MPI_Send() / MPI_Recv()
• MPI_Sendrecv()
• MPI_Sendrecv_replace()
• MPI_Put()
• MPI_Get()

NOTE:  In case you decide to use Cartesian topology (MPI_Cart_create(), MPI_Cart_sub()), keep in mind that for MPI dimension 0 is for 'columns' and 1 is for 'rows' (like in Fortran). For more information see here.

Questions. Here the steps you need to follow for the exercise submission:

1. Implement the distributed matrix-matrix multiply in double precision using the Fox Algorithm
2. Develop at least one test to show the correctness of your code, justify your test case.
3. Measure the performance of the code (execution time) for a square number of processes (that works with your matrix size) from 16 until 144 (or possibly 256) MPI processes and plot it.
4. Profile the code using Arm MAP when running with 144 (or possibly 256) processes, take a screenshot. Explain the observations.
5. Develop a performance model of the distributed matrix-matrix multiply and compare its results with the measurement and profiling. Discuss the comparison.